树
Golang 数据结构,树相关
1. 树
1.1 树形结构
现实中,有很多一对多的情况,如公司的行政架构图,文件系统中不同层级的文件,如果用链表这样的线性结构存储,显然很难做到,此时可以用树来表示
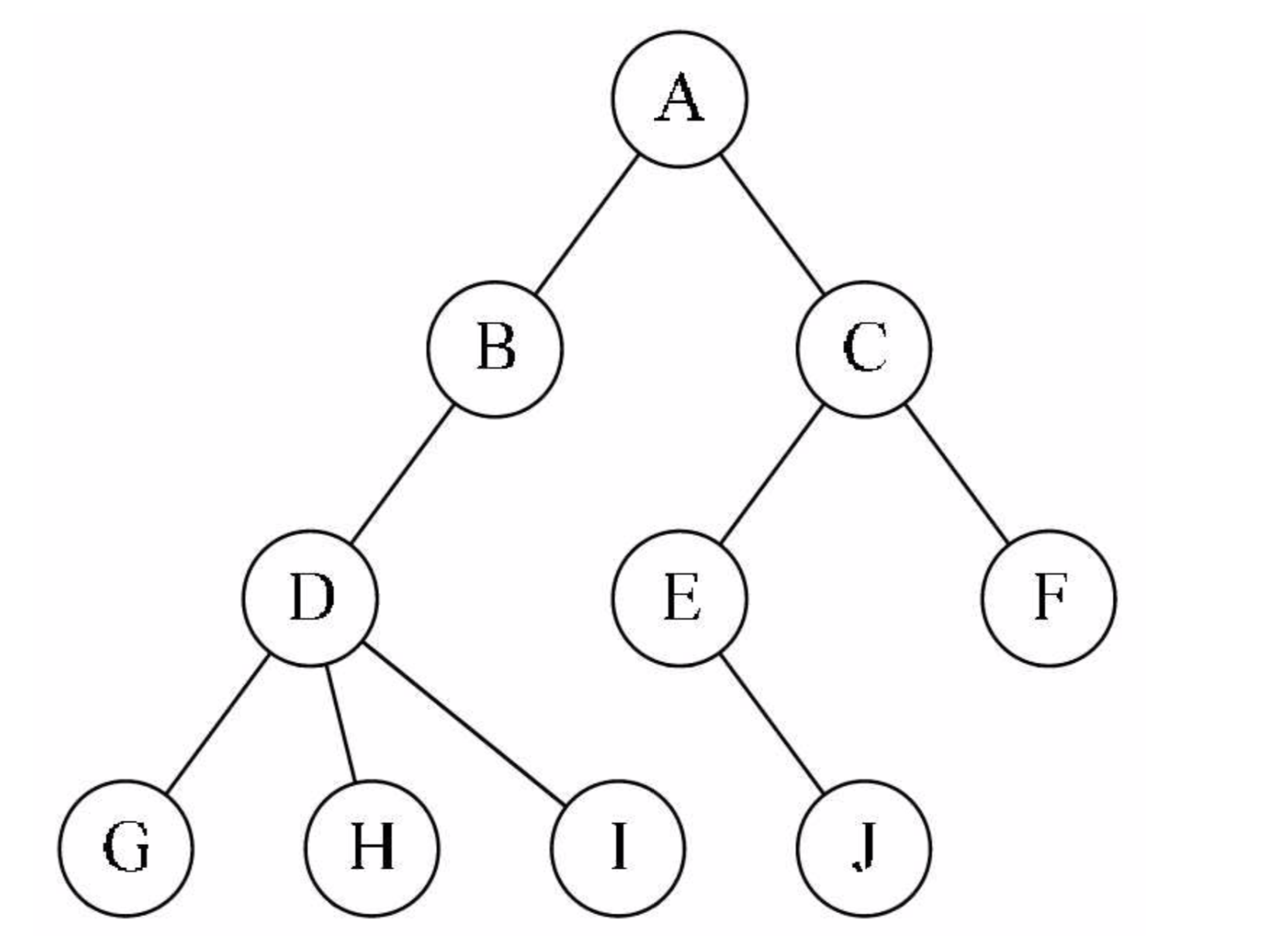
树(Tree)是一种 非线性数据结构,经常用来 存储具有层级关系的数据,它是 n(n>=0)个结点的有限集,n=0 时称为空树
在任意一棵非空的树中:
- 有且仅有一个特定的 根结点(Root)
- 当
n>1时,其余结点可分为m(m>0)个树,可以称为根的 子树(SubTree)
如图所示
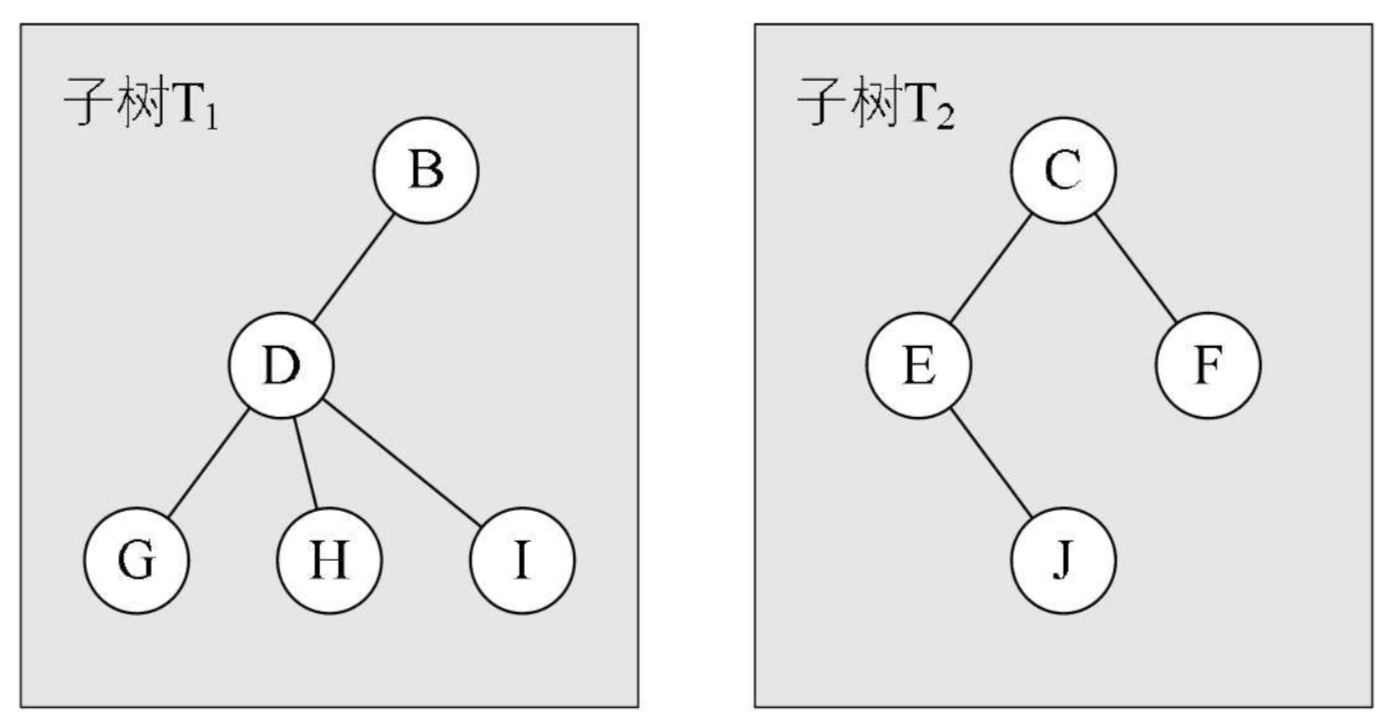
1.2 树的理解
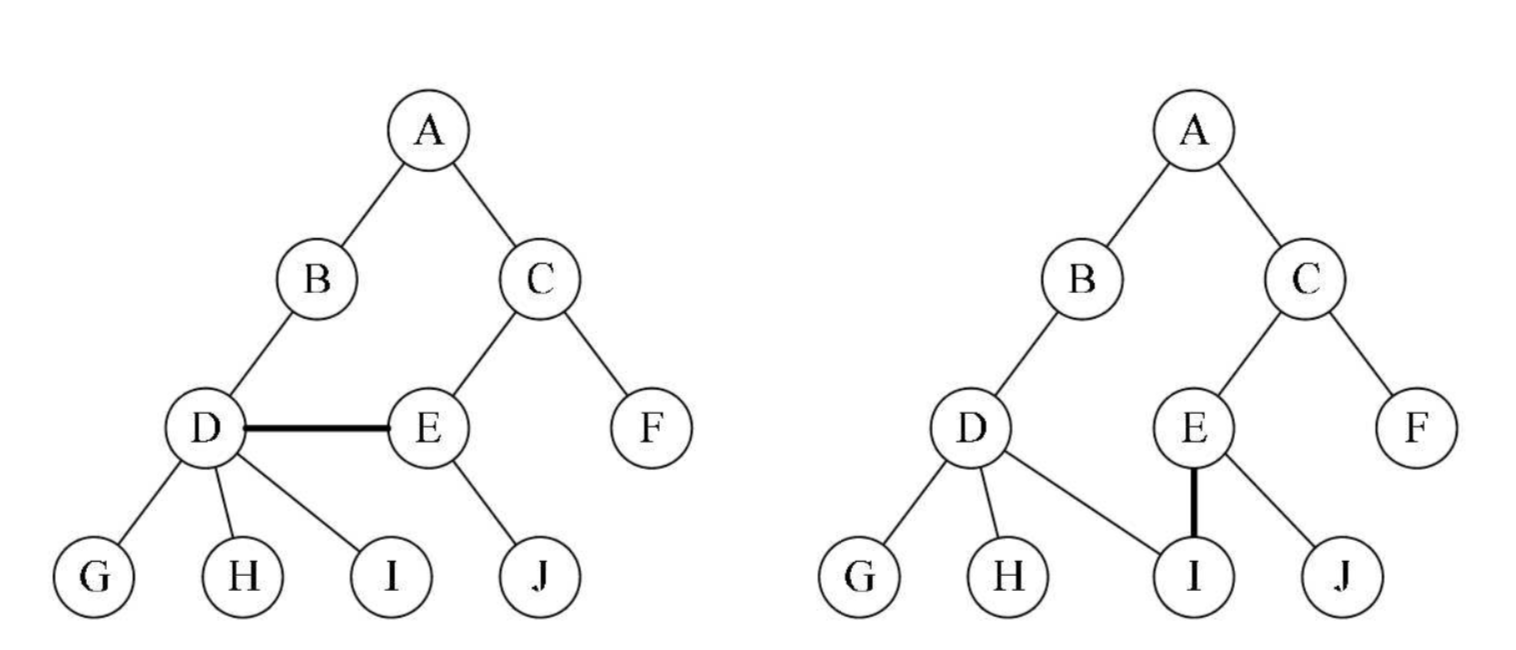
树的定义其实采用了 递归 的方法,如图所示,两个子树其实是根结点 A 的子树,当然 D,G,H,I 组成的树又是 B 为根结点的子树,以此类推:
除了要主要根结点的唯一性以外,子树之间一定是互不相交的,如下所示并不符合树的定义:
树的相关术语:
- 父结点:下方连接多个结点
- 子结点:父结点下的结点
- 结点的度(De-gree):拥有的子树数
- 叶结点(Leaf):没有子结点的结点,即 度为 0,也称为 终端结点
- 非叶结点:度不为 0 的结点,也称为 分支结点,也可以称为内部结点(根结点除外)
- 树的深度:从上往下定义,为叶结点所在 最大层数
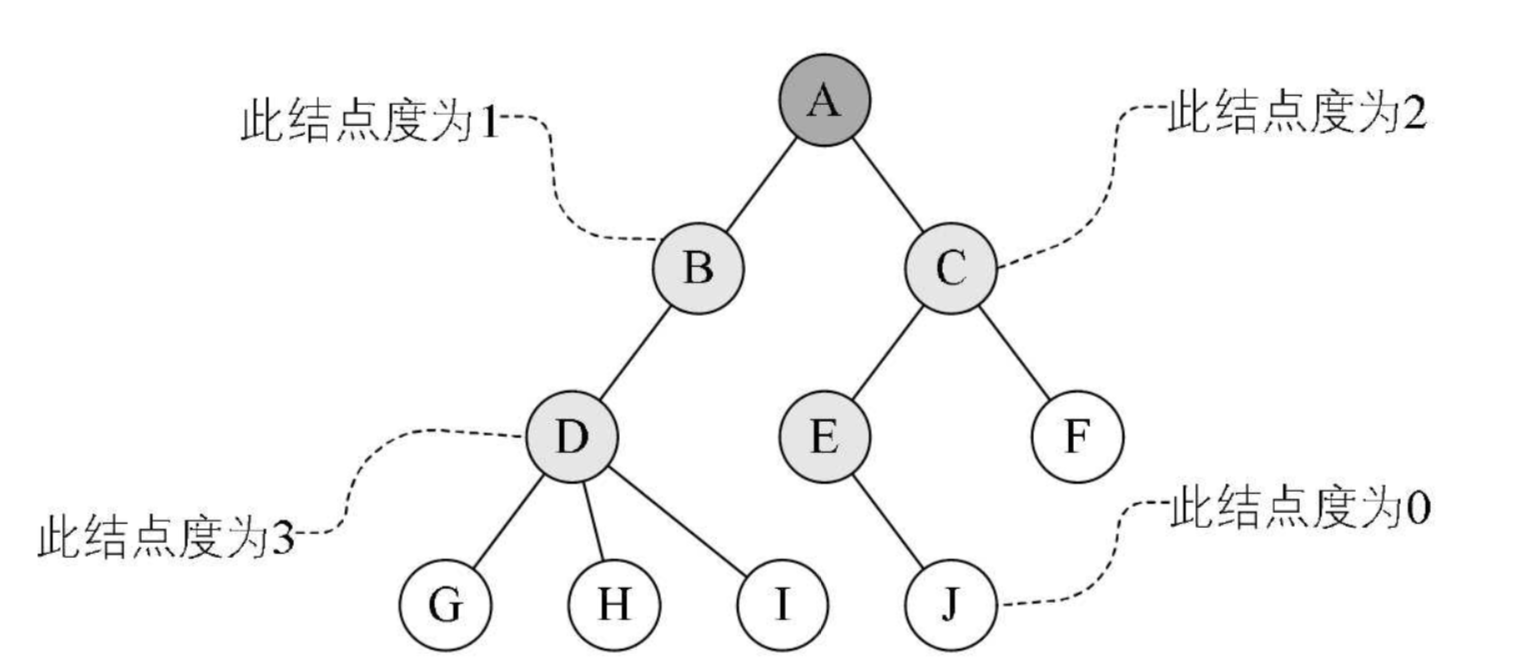
结点的层次(Level):根结点作为第一层,其孩子为第二层
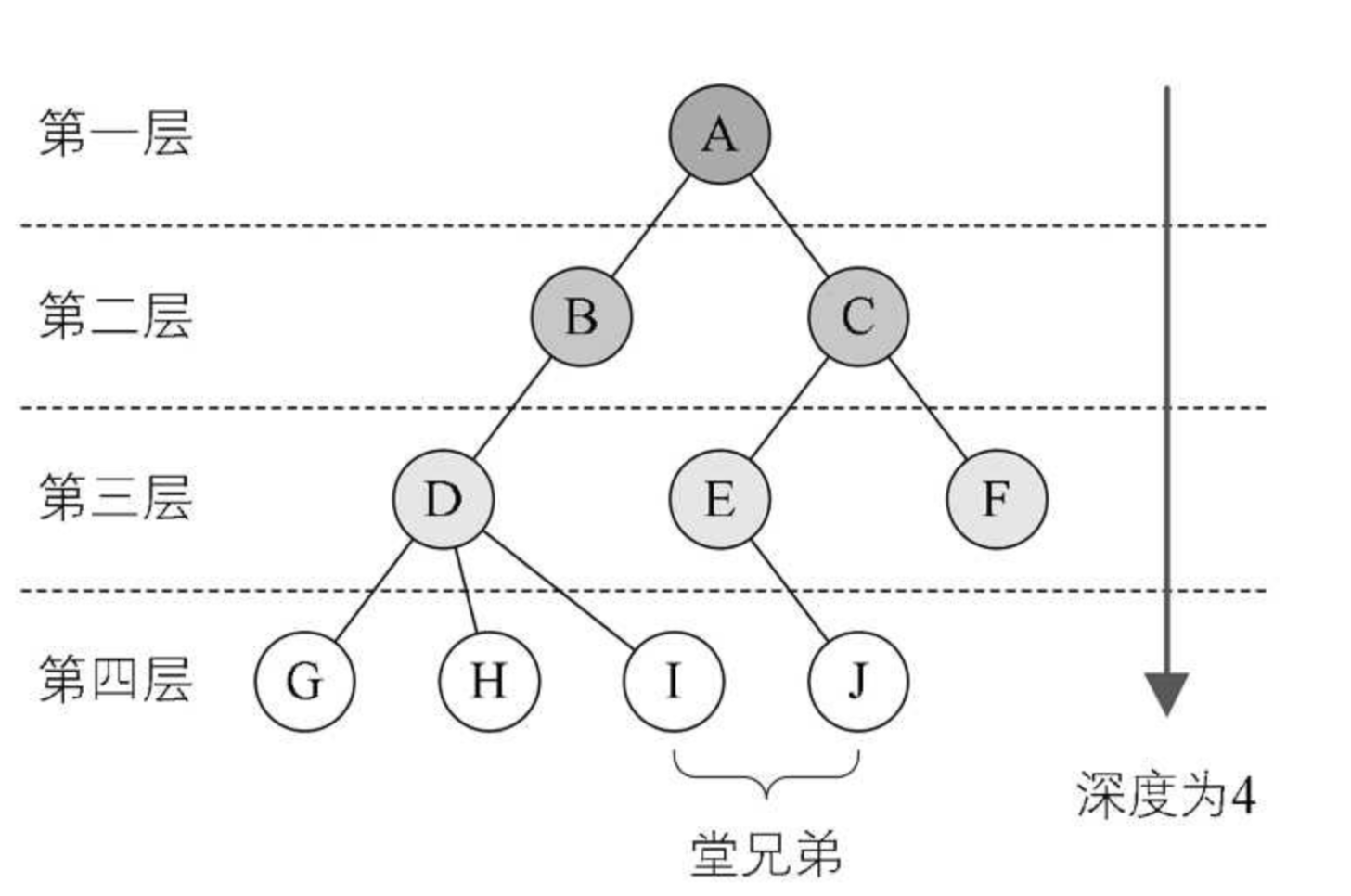
有序树与无序树:
- 有序树:树中的结点的各个子树看成从左至右有次序不可互换
- 无序树:与有序树相反
2. 树的存储结构
树的三种结构
由于树中的结点具备父子关系,使用顺序存储实现比较困难。树的存储结构主要有三种:
- 双亲表示法
- 孩子表示法
- 孩子兄弟表示法。
2.1 双亲表示法
树的每个结点不一定有孩子,但是 一定有且仅有一个双亲 结点(根结点除外),所以可以通过其双亲表示一个完整的树
// 树种的结点
type node struct {
data interface{} // 数据域:存储结点中的数据
parent int // 指针域:存储双亲在数组中的下标
}
// 树
type Tree struct {
nodes []*node // 结点指针数组
root int // 根结点位置
num int // 结点数
}其存储的数据格式如下:
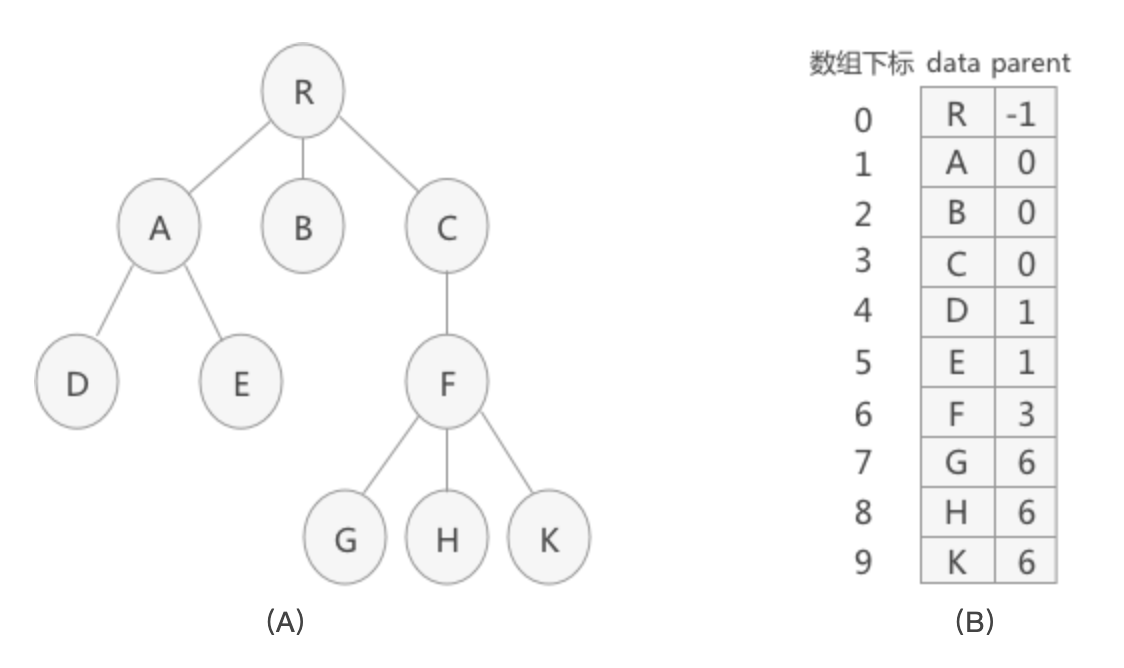
双亲表示法的优点:可以迅速找到当前结点的父结点,当 parent 为 -1 时,是根结点
双亲表示法的缺点:查找当前结点的子结点时,必须遍历整个树
- 缺点解决:增加一个结点的 最左孩子域,这样就能轻易得到结点的孩子
- 如果没有子结点,整个最左孩子域设置为 -1
- 但是如果孩子很多,超过 2 个,又需要关注结点的双亲、孩子、兄弟,那么需要不断的扩展结构,添加其他的域,比如:双亲域、左右兄弟域 等等
2.2 孩子表示法
把每个结点的孩子结点排列起来,以链表存储,如果树有 n 个结点,就会有 n 个链表,如果是叶结点,则此单链表为 空链表,然后 链表的头指针放在一个数组中
// 链表中的每个结点存储的不再是数据本身,而是数据在数组中的下标
type node struct {
child int // 数据域:数组下标 如 A、B、C 对应 1、2、3
next *node // 指针域:指向该结点的下一个孩子结点的指针
}
// 表头结构
type first struct {
data interface{} // 数据域:存储结点数据
first *node // 头指针域:存储该结点的孩子链表的头指针
}
// 树结构
type Tree struct {
nodes []*node
root int
num int
}孩子表示法如图所示:
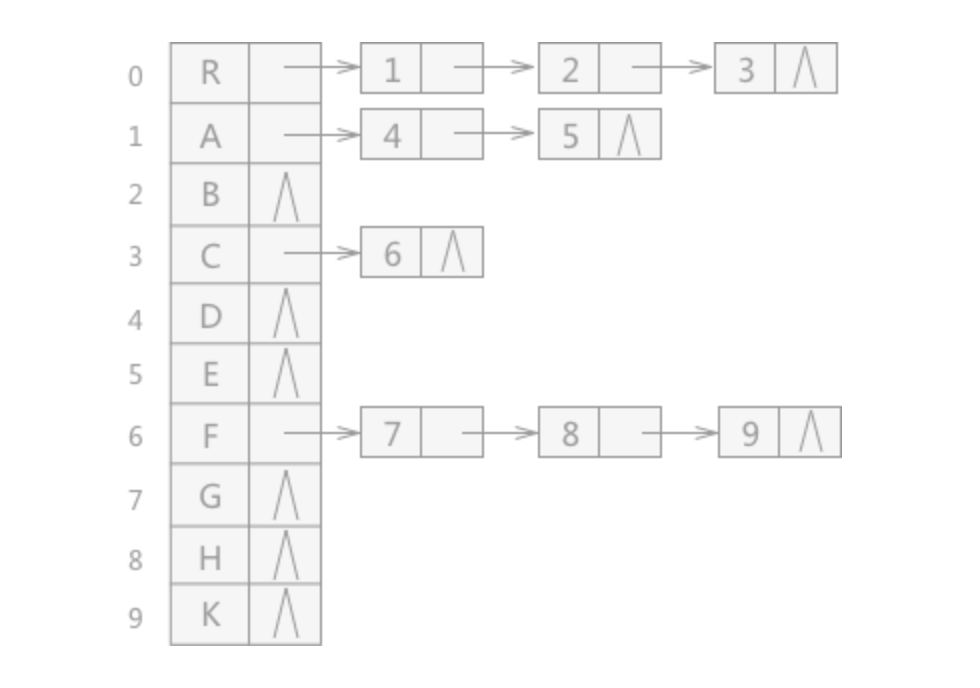
适用于查找某结点的孩子结点,不适用于查找其父结点
相当于用树的结构体中的 nodes,把每个结点像数组一样存起来,再额外加指针,关联(链式指向)其所有子结点,每个结点通过数组下标再次关联,形成完整结构(感觉本质还是以顺序存储为媒介,混合了链式关联的结构)
可以将两种表示方法合二为一,存储效果如图:
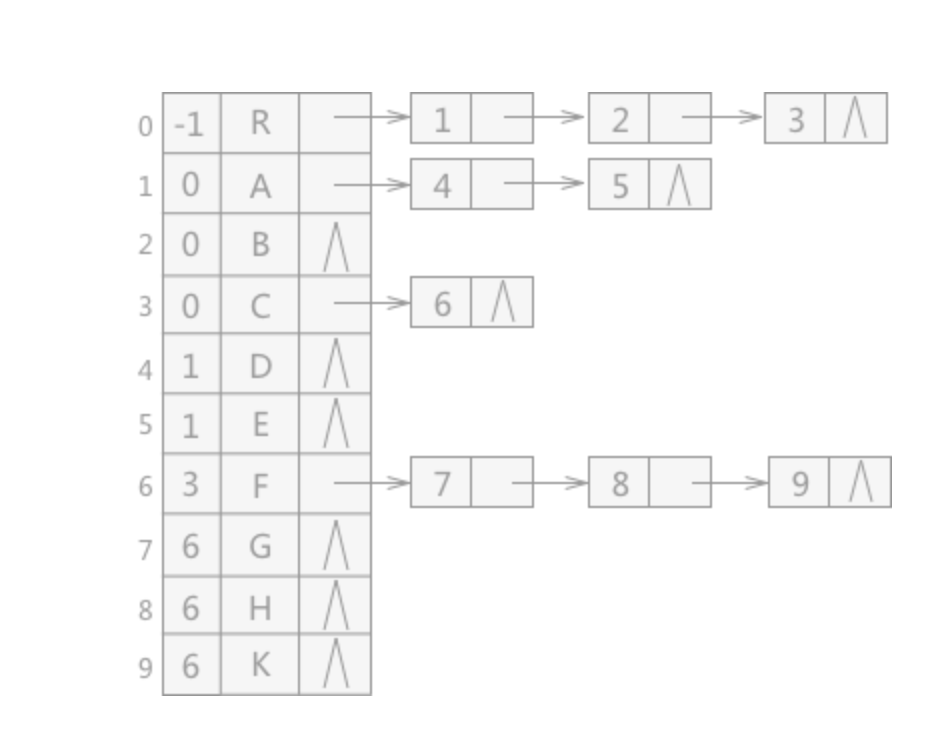
再对每个 node 加个 parent 变量,来存储每个结点的父结点
2.3 孩子兄弟表示法
任意一棵树,它的结点的第一个孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的,因此设置两个指针,分别指向该结点的 第一个孩子 和此结点的 右兄弟 即可
type node struct {
data interface{}
firstchild *node
rightchild *node
}如图所示:
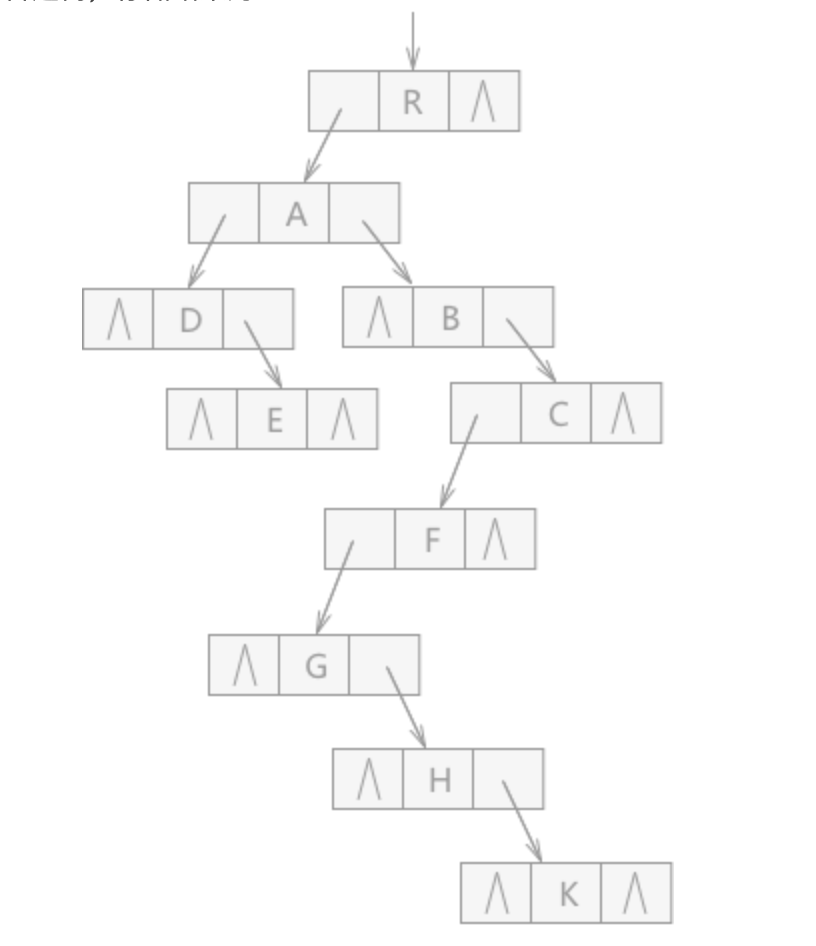
上述的表示方法,给查找某个结点的某个孩子带来了方便,只需要通过 firstchild 找到此结点的长子,然后再通过长子结点的 rightsib 找到它的二弟,依次类推,直到找到具体的孩子
当然如果要找到双亲,依然有困难(添加 parent 指针域可以解决)
孩子兄弟表示法其实是 将一棵 复杂的树 表示为了 二叉树
3. 二叉树
二叉树(Binary Tree): 树的每个结点的度最大为 2,即最多拥有 2 棵子树
二叉树有五种形态:
- 空二叉树
- 只有一个根结点
- 根结点只有左子树
- 根结点只有右子树
- 根结点既有左子树又有右子树
注意:二叉树的 左子树和右子树是有顺序的,不能任意颠倒,即使树种某个结点只有一棵子树,也要区分它是左子树还是右子树。交换左右子树后生成的新二叉树就不再是以前的二叉树了!!所以二叉树是 有序树!
一些特殊的二叉树:
- 斜树:斜树看起来类似线性结构,有左斜树(只有左侧结点),右斜树(只有右侧结点),此时 结点的个数就是二叉树的深度
- 真二叉树(Proper Binary Tree):所有结点的度要么为 0,要么为 2
- 满二叉树(Full Binary Tree):所有结点的度要么为 0,要么为 2,且叶结点都在最后一层(其实是在 真二叉树 基础上添加了限制)
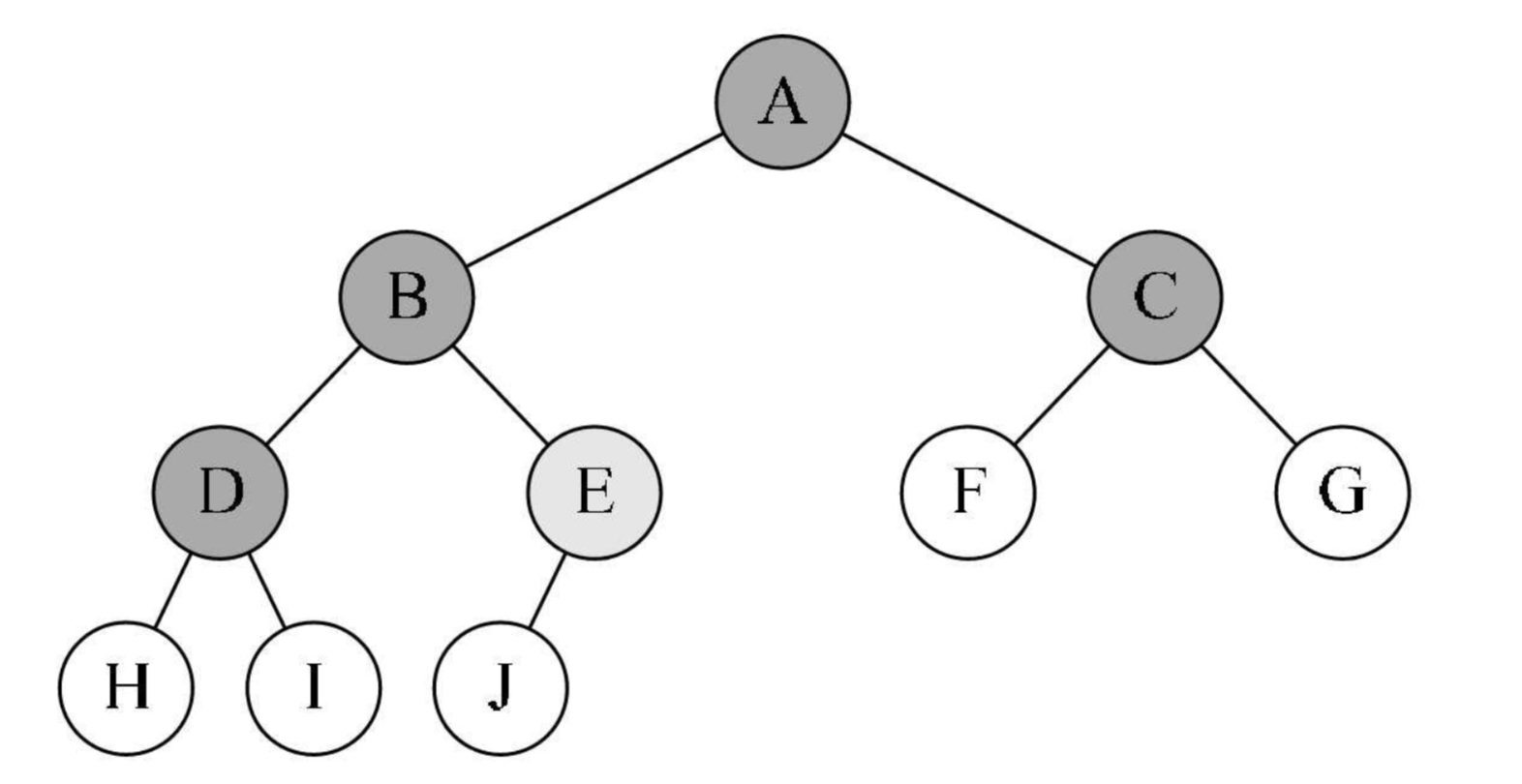
3.1 非空二叉树的特性
- 每层结点数:二叉树的第 i 层上至多有 2i-1 个 结点 (i>=1)
- 全部结点数:高度为 h 的二叉树至多有 2k-1 个结点 (h>=1,也是叶结点所在的最大层数) 相应的高度 h = log$_2$n+1
- 叶结点数与度关系:叶结点数 = 度为 2 结点数 + 1
叶结点与度关系推导:
# n0 是叶结点数,n1 是度为1的结点数,n2 是度为2的结点数,T为二叉树的结点连线总数:
T = 1*n1 + 2*n2
T = n - 1
n = n0 + n1 + n2其实还可以得到一个公式: n = 2n0 + n1 - 1
如图所示:
3.3 完全二叉树
完全二叉树(Complete Binary Tree):叶子结点只会出现在最后 2 层,且最后 1 层的叶子结点都靠左对其
如图:
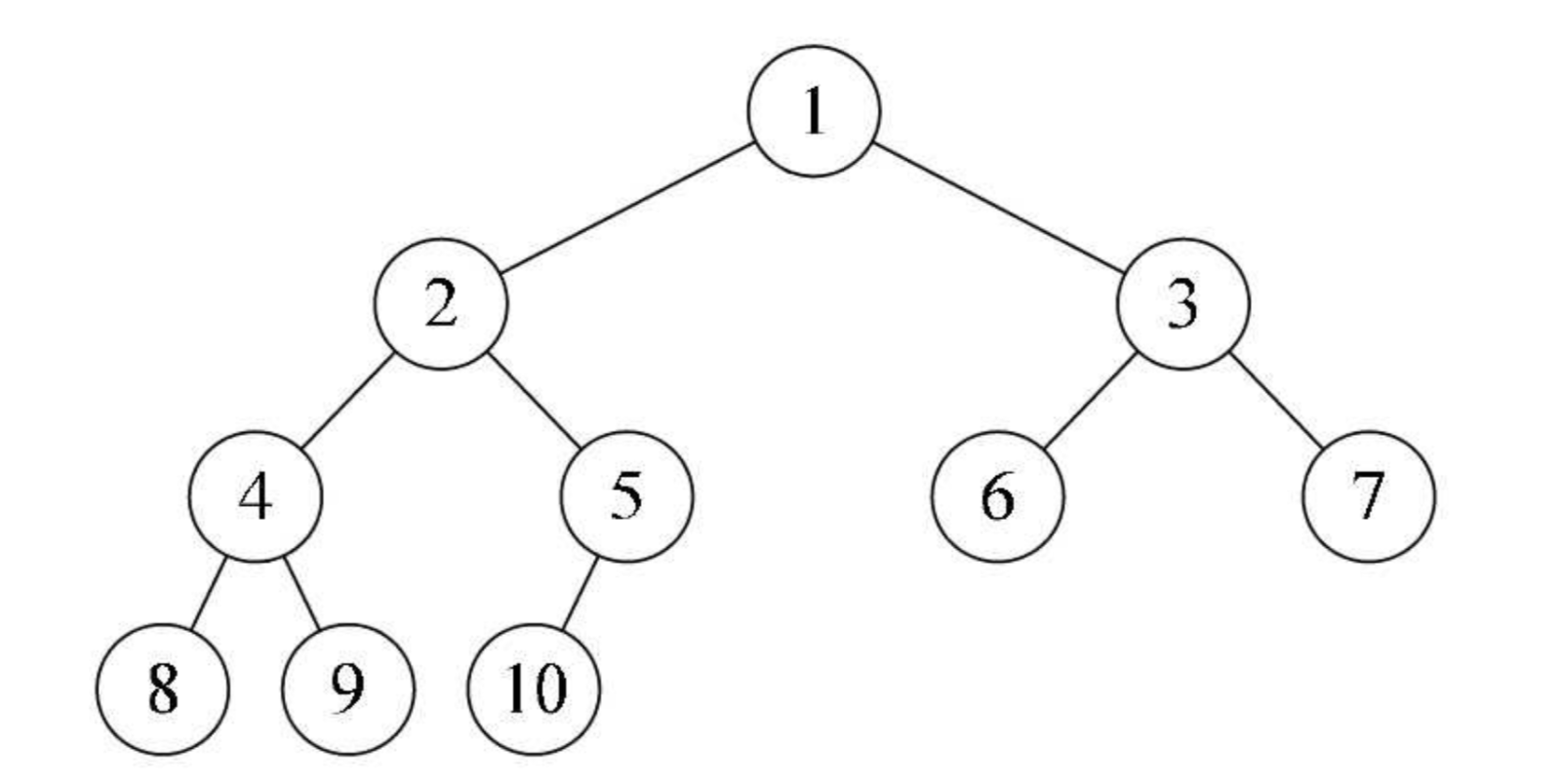
注意:完全二叉树不一定是满的,但是只要将完全二叉树补充上对应子结点,就是一棵满二叉树。
也可以推理出:
- 满二叉树一定是完全二叉树
- 完全二叉树的根结点到倒数第二层之间的树是一棵满二叉树
特性
完全二叉树的特点:
- 度为 1 的结点只有左子树
- 度为 1 的结点要么是 1 个,要么是 0 个
- 同样结点数的二叉树,完全二叉树深度最小
- 如果结点度为 1,则该结点只有孩子结点,不存在只有右子树的情况
假设完全二叉树的高度为 h ,h >= 1,则:
- 则至少有 2h-1 个结点
- 则最多有 2h - 1 个结点 (满二叉树)
总结点数量 n :
- 则:2h - 1 <= b < 2h
- 也即 h - 1 <= log2n < h,由于 h 是整数,h = floor(log2n) + 1 (向下取整)
n0 是叶结点数,n1 是度为 1 的结点数,n2 是度为 2 的结点数:
# 二叉树本身的规律
n = 2n0 + n1 - 1
# 完全二叉树的n1要么是1,要么是0一颗有 n(n>0) 个结点的完全二叉树,从上到下,从左到右,给结点从 1 编号,则第 i 个结点有:
- i=1,是根结点
- i>2,其父结点编号是 floor(i/2)
- 2i<=n,其左子结点编号为 2i
- 2i>n,则其无左子结点
- 2i+1<=n,则其右子结点编号为 2i+1
- 2i+1>n,则其无右子结点
3.4 二叉树存储结构
树使用顺序存储是非常困难的,但是二叉树结构特殊,使用顺序存储也能实现,即:用一维数组存储二叉树中的结点和结点关系
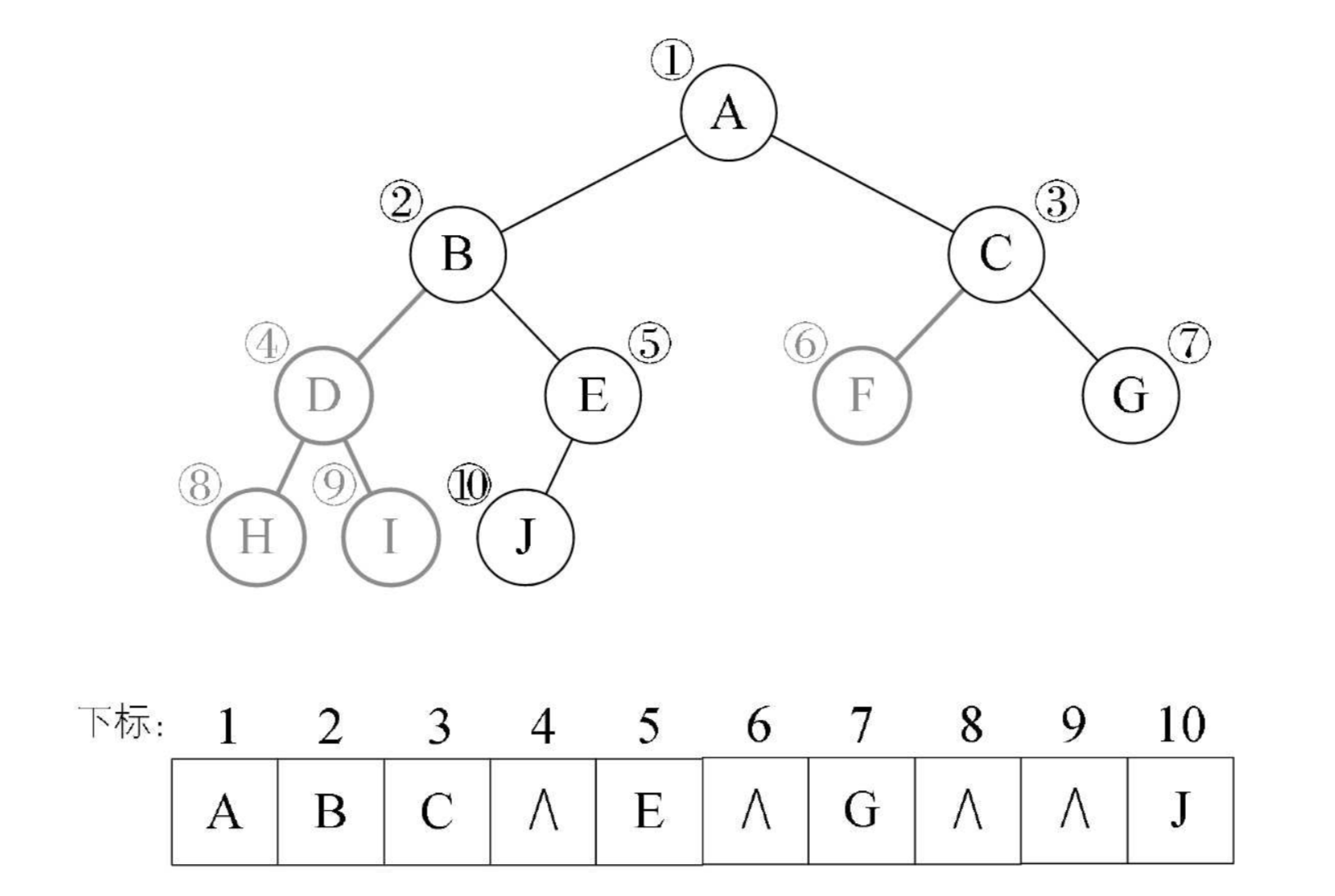
图中 4,6,8,9 结点不存在。顺序存储虽然能够表述二叉树,但是实用性不强,比如一种极端的情况,树的深度为 k,但是是右倾斜树,只有 k 个结点,却需要分配 2k-1 个存储单元,造成了空间的极大浪费
推荐使用链式存储,即二叉链表:每个结点最多有两个孩子,结点分别设计一个数据域、两个指针域,即可表示一个结点
type node struct {
data interface{}
lchild *node
rchild *node
}二叉链表示意图:
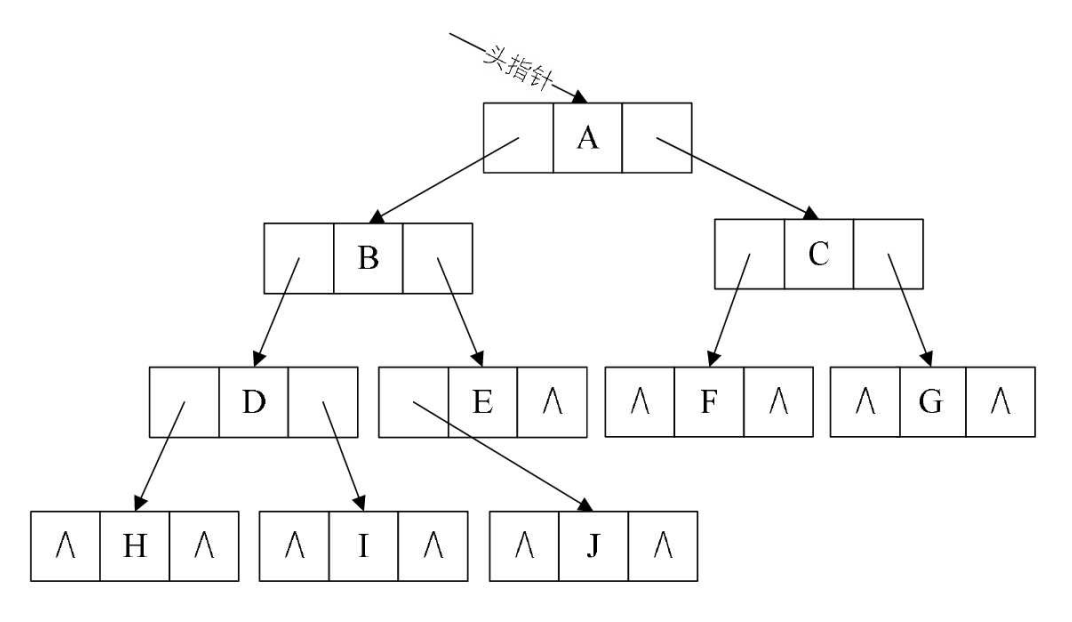
3.5 二叉树的四种遍历方式
二叉树要对其遍历如图:
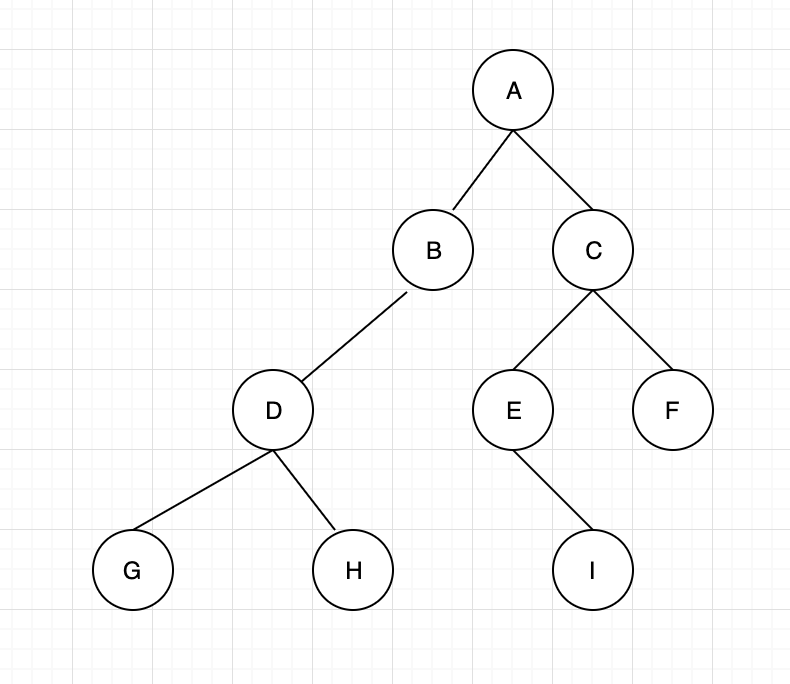
遍历一般是 从根结点开始,当然我们也可以限制左右顺序遍历是从左开始,主要遍历方法有下列多种:
前序遍历(Preorder Traversal):根结点 -> 前序遍历左子树 -> 前序遍历右子树
- 结果为
A -> BDGH -> CEIF
- 结果为
中序遍历(Inorder Traversal):中序遍历左子树 -> 根结点 -> 中序遍历右子树
- 结果为
GDHB -> A -> EICF
- 结果为
后序遍历(Postorder Traversal):从左到右遍历左子树叶结点 -> 从左到右遍历右子树叶结点 -> 根结点
- 结果为
GHDB -> IEFC -> A
- 结果为
层序遍历(Level Order Traversal):根结点 -> 第一层 -> 第二层 -> ... 依次类推
- 结果为
A -> BC -> DEF -> GHI
- 结果为
3.6 实现
二叉树的定义和遍历都需要利用递归原理
package main
import (
"fmt"
"reflect"
)
type BinaryTree struct {
data interface{}
left *BinaryTree
right *BinaryTree
}
func NewBinaryTree(e interface{}) *BinaryTree {
return &BinaryTree{
data: e,
left: nil,
right: nil,
}
}
func Appoint() *BinaryTree {
/*手动指定如上图的一颗树
A
B C
D E F
G H I
*/
A := NewBinaryTree("A")
B := NewBinaryTree("B")
C := NewBinaryTree("C")
D := NewBinaryTree("D")
E := NewBinaryTree("E")
F := NewBinaryTree("F")
G := NewBinaryTree("G")
H := NewBinaryTree("H")
I := NewBinaryTree("I")
A.left = B
A.right = C
B.left = D
D.left = G
D.right = H
C.left = E
C.right = F
E.right = I
return A
}
// 对于所有的树来说,遍历都是通用的
// 前序遍历
func PreOrderTraverse(t *BinaryTree) {
if t == nil {
return
}
fmt.Print(t.data) // 前序遍历就是从node开始遍历,所以要先打印 ABDGHCEIF
PreOrderTraverse(t.left)
PreOrderTraverse(t.right)
}
func InOrderTraverse(t *BinaryTree) {
if t == nil {
return
}
// 会产生式升序结果 GDHBAEICF
InOrderTraverse(t.left)
fmt.Print(t.data)
InOrderTraverse(t.right)
// 会产生降序结果 FCIEABHDG
//InOrderTraverse(t.right)
//fmt.Print(t.data)
//InOrderTraverse(t.left)
}
// 后序遍历
func PostOrderTraverse(t *BinaryTree) {
if t == nil {
return
}
PostOrderTraverse(t.left)
PostOrderTraverse(t.right)
fmt.Print(t.data) // GHDBIEFCA
}
func main() {
t := Appoint()
fmt.Println(t, reflect.TypeOf(t))
PreOrderTraverse(t)
fmt.Println()
InOrderTraverse(t)
fmt.Println()
PostOrderTraverse(t)
}二叉树递归缺陷
每次递归调用都会开辟一个函数栈空间,递归次数很多时,就会出现内存的急剧消耗,所以 最好的遍历方式仍然是迭代方式遍历
迭代方式实现遍历与层序遍历的思路相似,都需要借助一个数据结构来实现,一般是 栈 或 队列
层序遍历
使用队列,将根节点入队,循环(队列为空则表示所有结点出队完成),从根结点开始,对出的同时,将其左右子结点入队
import (
"container/list"
)
func LevelOrderTraverse(t *BinaryTree) {
if t == nil {
return
}
queue := list.New()
queue.PushBack(t)
// 循环,将一层层的父结点出队,关联子结点依次入队
for queue.Len() != 0 {
queueHead := queue.Remove(queue.Front()) // 队首出队 即上文入队的t
tempNode:= queueHead.(*BinaryTree) // 类型断言
fmt.Print(tempNode.data)
if tempNode.left != nil {
queue.PushBack(tempNode.left)
}
if tempNode.right != nil {
queue.PushBack(tempNode.right)
}
}
}遍历的应用
层序遍历可以用来:
- 计算二叉树的高度
- 判断一棵树是否为完全二叉树
通过前序/后续遍历 + 中序遍历的结果也可以推导出唯一的一棵二叉树:
- 前序遍历总是从 root 结点开始:根结点 -> 左子树 -> 右子树,此时可以找到其根结点 ,前缀定左
- 中序遍历从是从左子树开始:左子树 -> 根结点 -> 右子树,从前序遍历已经知道了根结点位置,依据中序就能知道其左右子结点 中缀定左右
二叉树与四则运算
四则运算(+、-、*、/)一般有三种:
- 前缀表达式(prefix expression),也称为波兰表达式
- 中缀表达式(infix expression),该方式符合人类的视觉思维
- 后缀表达式(postfix express),又称为逆波兰表达式
所谓的前缀、后缀、中缀指的是运算的位置是在两个操作数的左中右位置,如下所示:

func Appoint2() *BinaryTree {
A := NewBinaryTree("+")
B := NewBinaryTree("9")
C := NewBinaryTree("*")
D := NewBinaryTree("-")
E := NewBinaryTree("2")
F := NewBinaryTree("4")
G := NewBinaryTree("1")
A.left = B
A.right = C
C.left = D
C.right = E
D.left = F
D.right = G
return A
}如果将四则运算表达式的操作数作为叶子结点,运算符作为父结点,则可组成一棵二叉树,如 A / B + C * D - E:
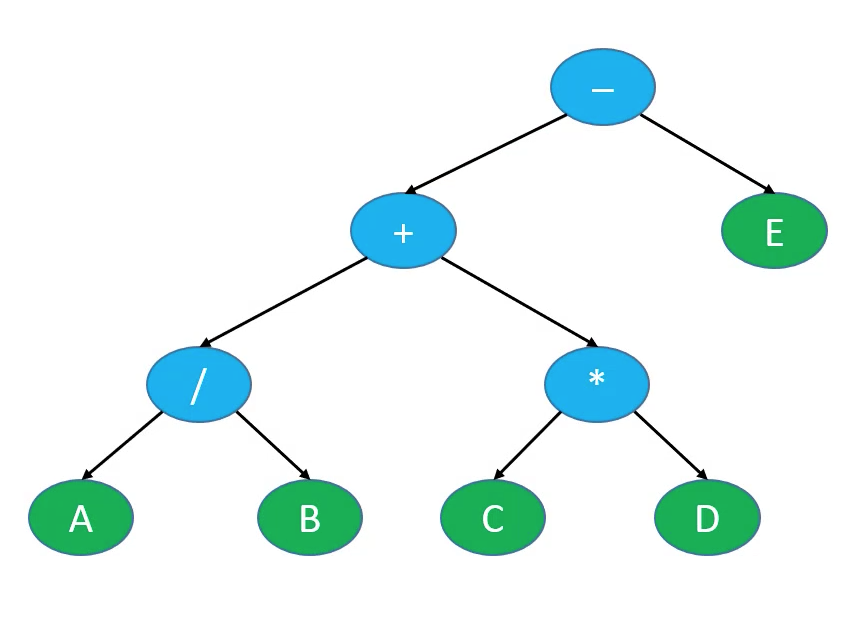
如果对该二叉树进行前序遍历,就会生成前缀表达式。如果进行中序遍历,则会生成中缀表达式,同理进行后序遍历,则生成后缀表达式
4. 二叉搜索树
二叉搜索树 BST(Binary Search Tree),也称为 二叉排序树,二叉查找树
二叉搜索树可以为空。如果不为空,则满足:
- 非空左子树的所有键值小于其根结点的键值
- 非空右子树的所有键值大于其根结点的键值
- 左、右子树本身也都是二叉搜索树
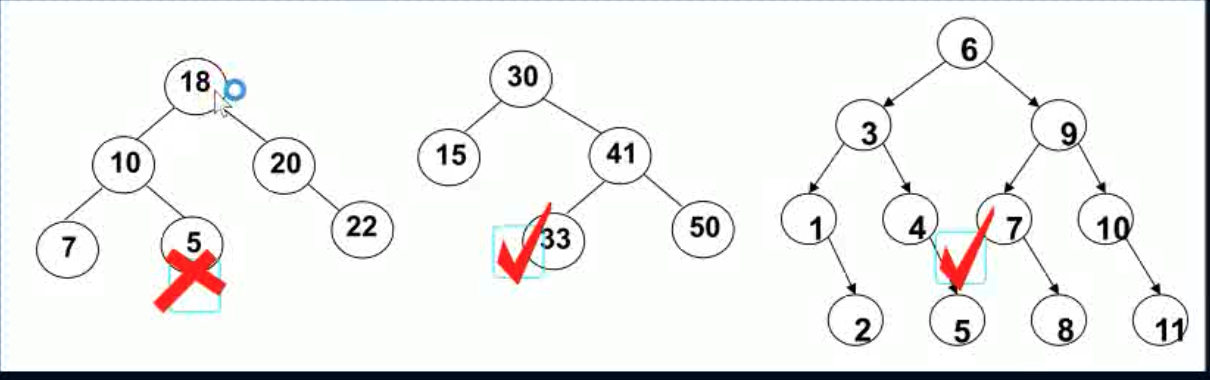
如图所示,红勾表示的即是二叉搜索树:
4.1 二叉搜索树查找思想
如其名称定义,二叉搜索树的查找很便利。如果要对下列混乱的数据进行查找 7 是否在数据中:{1,3,6,7,9,0,4,2,5,8}。对这种无序的数据,我们可以使用循环操作挨个遍历,或者使用 哈希表 方式
如果现在要对一个有序的数据进行查找{0,1,2,3,4,5,6,7,8,9},可以使用二分查找即可快速找出 7 是否在数据中。
其实这和二叉搜索树的概念是一致的,利用折半的思想,这个数据序列转换为二叉搜索树后如图:
二叉搜索树与哈希表作为查找时的对比:
- 哈希表需要一个很大的数组,会造成一定的空间浪费
- 哈希表的数据是无序的,二叉搜索树其实是有序数据利用二分查找思想的转换
二叉搜索树在插入结点的时候,也需要一层层比较大小,由此也带来新的特性:很容易获取最大值,最小值
注意
其实二叉搜索就是二分搜索法的是数据结构实现,中序遍历可以得到从小到大的结果!!(右左逆序则从大到小)
4.2 插入实现
递归插入
package main
import (
"fmt"
"math/rand"
"time"
)
type BSTree struct {
data int
left *BSTree
right *BSTree
parent *BSTree // 记录父结点的原因是便于删除操作,以及对红黑树的演化
}
func NewBSTree(e int) *BSTree {
return &BSTree{
data: e,
left: nil,
right: nil,
parent: nil,
}
}
// 递归实现
func InsertRC(bst *BSTree, e int) *BSTree {
if bst == nil {
return NewBSTree(e)
}
if e < bst.data {
bst.left = InsertRC(bst.left, e)
bst.left.parent = bst
}
if e > bst.data {
bst.right = InsertRC(bst.right, e)
bst.right.parent = bst
}
return bst
}
func InOrderTraverse(tree *BSTree) {
if tree == nil {
return
}
InOrderTraverse(tree.left)
fmt.Print(tree.data, " ")
InOrderTraverse(tree.right)
}
func main() {
rand.Seed(time.Now().UnixNano())
arr := []int{}
for i := 0; i < 20; i++ {
arr = append(arr, rand.Intn(100))
}
fmt.Println(arr)
var head *BSTree
for _, item := range arr {
head = InsertRC(head, item)
}
InOrderTraverse(head)
}循环指针插入
遍历形式插入,类似于链表通过 链式指针 p 不断比较遍历至空结点再进行插入操作
package main
import (
"fmt"
"math/rand"
"reflect"
"time"
)
type TreeNode struct {
data int
left *TreeNode
right *TreeNode
parent *TreeNode // 便于删除
}
func NewTreeNode(e int) *TreeNode {
return &TreeNode{
data: e,
left: nil,
right: nil,
parent: nil,
}
}
// BSTree 二叉搜索树对象
type BSTree struct {
root *TreeNode
length int
}
func NewBSTree() *BSTree {
return &BSTree{
root: nil,
length: 0,
}
}
// Insert 插入元素:迭代方式
func (bst *BSTree) Insert(e int) {
if bst.root == nil {
bst.root = NewTreeNode(e)
bst.length++
return
}
p := bst.root
for p != nil {
if e < p.data {
if p.left != nil {
p = p.left
} else {
p.left = NewTreeNode(e)
p.left.parent = p
break
}
} else if e > p.data {
if p.right != nil {
p = p.right
} else {
p.right = NewTreeNode(e)
p.right.parent = p
break
}
} else {
break
}
}
bst.length++
return
}
func InOrderTraverse(root *TreeNode) {
if root == nil {
return
}
InOrderTraverse(root.left)
fmt.Print(root.data, " ")
InOrderTraverse(root.right)
}
func main() {
rand.Seed(time.Now().UnixNano())
arr := []int{}
for i := 0; i < 20; i++ {
arr = append(arr, rand.Intn(100))
}
fmt.Println(arr)
bst := NewBSTree()
fmt.Println(bst, reflect.TypeOf(bst))
for _, item := range arr {
bst.Insert(item)
}
InOrderTraverse(bst.root)
fmt.Println("\nNon -repeatable tree length is:", bst.length)
}若数据重复,每个结点还需添加额外字段 count 可以用来计数
二叉搜索树的 ADT
对于二叉搜索树来说,只需要保存根结点即可,因为其他结点都可以通过根结点找到。
二叉树的结点内部必须保留左右子结点信息,若保留了父结点信息,更便于删除操作,此外 还可以用无父结点的二叉搜索树
4.3 二叉搜索树其他操作
// 判断存在元素 (查找思路一致)
func (bst *BSTree)hasElement(e int) bool {
p := bst.root
for p != nil {
if e > p.data {
p = p.right
}else if e < p.data {
p = p.left
} else {
return true
}
}
return false
}
// 获取最小值 (最大值思路一致)
func (bst *BSTree) getMin() interface{} {
p := bst.root
var data interface{}
for p != nil {
data = p.data
p = p.left
}
return data
}
func main() {
//...
fmt.Println("Min Value:", bst.getMin())
fmt.Println("has 13:", bst.hasElement(13))
}查找结点的前驱
前驱结点其实就是中序遍历时,当前结点的前一个结点,即从左侧找,会找到小一点的数据,该数据一定是删除结点左子树的最大值,称之为 前驱
假设要当前结点为 n ,则查找时有三种情况
node.left == nil && node.parent == nil- 前驱为:无前驱结点
node.left == nil && node.parent != nil- 前驱为:node.parent.parent.parent....
- 终止条件为:node 在 parent 的右子树中
n.left != nil- 前驱为:node.left.right.right.right...
- 终止条件为:right 为 nil
查找结点的后继
后继结点其实就是中序遍历时,当前结点的后一个结点,即从右侧找,会找到大一点的数据,该数据一定是删除结点右子树的最小值,称之为 后继
假设当前结点为 n ,则查找有三种情况
node.right == nil && node.parent == nil- 后继为:无后继结点
node.right == nil && node.parent != nil- 后继为:node.parent.parent.parent....
- 终止条件为:node 在 parent 的左子树中
n.right != nil- 后继为:node.right.right.right.right...
- 终止条件为:left 为 nil
删除结点
删除结点对应需要先确定结点是否存在,即找到值对应的结点,然后依据找到的结点的不同,执行不同的操作:
- 度为 0 结点: 直接删除 即可,如果删除的结点也是根结点,则还需要将根结点掷空
- 度为 1 结点: 使用子结点替换原结点,如果删除的结点也是根结点,则还需将根结点指针指向子结点
- 如果删除的结点只有左子结点:
child.parent = node.parent node.parent.left = child - 如果删除的结点只有右子结点:
child.parent = node.parent node.parent.right = child
- 如果删除的结点只有左子结点:
- 度为 2 结点: 使用期前驱/后继替换当前结点,然后删除刚才替换的前驱/后继
对于度为 2 的结点,其左子树的结点都小于它,右子树的结点都大于它!!按照二叉搜索树这个特性,取代被删除结点位置的结点值必须仍然比左子树都大,并比右子树都小,这样的结点正好是其前驱/后继。删除度为 2 结点的问题到这里就演变为了:找到要删除结点的前驱来替换掉当前位置,或者找到后继来替换掉当前位置,最后删除前驱或者后继。其前驱、后继结点的度必定为 0 或者 1,此时再删除前驱、后继就变得简单了!
如图所示的二叉搜索树:
如果不是叶结点,那么会有相当多的麻烦,尤其是被删除结点拥有多个子结点:
- 删除结点 9:将 8 替换到 9,或者将 10 替换到 9 即可
- 删除结点 7:有两种方式
- 左侧查找,用 5 替换位置 7,此时 3 依然指向 5,5 的 right 需要指向 9
- 右侧查找,用 8 替换位置 7,此时 8 的 left 是 5,right 是 9
- 删除结点 15:也有从左侧、右侧查找两种方式
- 右侧查找:用 18 替换位置 15,20 的 left 指向 19
4.4 时间复杂度与平衡树
二叉搜索树其实就是 二分查找法 的数据结构实现,其时间复杂度大致为:O(logn)
二叉搜索树的缺陷
但是如果二叉搜索树在插入时,如果相继插入的 数据都是有序 的,会造成树形成一个 类似链表 的结构 ,按照下列规则添加:
9,8,7,6,5,4,3,2,1那么此时二叉搜索树就会像 链表 一样存在,其查找速度也会变化为 O(n),引起查找的极大性能缺失,这种插入连续数据形成的 分布不均匀的二叉树 为 非平衡树(No-Balance) 只有 平衡二叉搜索树 才能更加符合实际的业务需求
- 对于一棵平衡二叉树,查找操作效率是 O(logn)
- 对于一棵非平衡二叉树,相当于编写了一个链表,查找效率上升为 O(n)
为了避免这种现象,即保证树是平衡的,就要让树的 每个结点的左边子孙结点个数尽量等于右边的子孙结点的个数
平衡二叉搜索树
如果要让链表一样的二叉搜索树恢复平衡,其做法一般是 缩小树的高度,即 让左右子树的高度都尽量接近或者一致,这样达到平衡的二叉搜索树,我们称之为 平衡二叉搜索树(Ballanced Binary Search Tree)
常见的平衡二叉搜索树有:
- AVL 树: Windows 操作系统常用
- B+ 树: 数据库索引使用
- 红黑树: 最重要的平衡二叉搜索树,C++ 的 STL 库,Java 中的哈希表(碰撞超过 8 个时,链表转换为红黑树)
AVL树
AVL 树是早期的 平衡树,可以实现树的平衡,因为其每个结点 多存储了一个额外的数据,插入/删除效率不及红黑树,所以整体效率不及红黑树